Des réactions parfois contradictoires venant d’enseignants ou d’observateurs ont circulé dans les réseaux sociaux à propos de la compétence dans l’épreuve de mathématiques. Dans une plateforme WhatsApp, un inspecteur de l’éducation a partagé son appréciation au deuxième jour du Cfee, en ces termes : «A lire certaines épreuves du Cfee, je me suis dit que celles-ci ont beaucoup perdu en niveau de difficulté… Il y a une sorte de culture du moindre effort de plus en plus en partagée. Je crois qu’il faut tirer le système par le haut en proposant des évaluations de plus en plus complexes, au fil des prochaines sessions, pour secouer maîtres et élèves.» D’autres ont partagé des appréciations différentes, du genre : «Cette épreuve est très complexe et compliquée pour des enfants de 12 ans.»

Ainsi, il nous paraît important de faire un débat basé sur des arguments pédagogiques et didactiques, afin de faire comprendre les enjeux et faire évoluer les représentations pour un meilleur encadrement de nos élèves, en dehors de toute posture subjective.

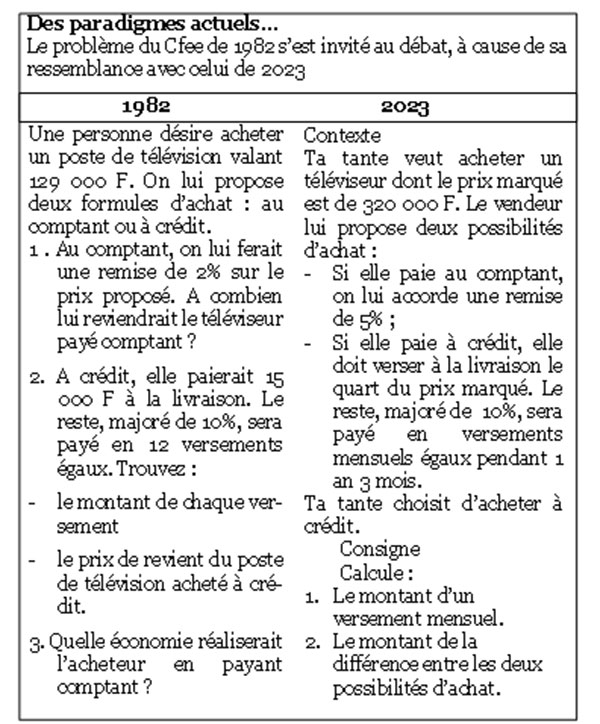
Voici un bel exemple pour comprendre le changement de paradigme.
Avant l’introduction de l’Apc (problème de 1982), les questions intermédiaires étaient posées à l’élève ; dans le fil conducteur de la résolution, l’évaluateur lui tenait la main, pas à pas. Son autonomie est très limitée.

Avec l’Apc (problème de 2023), la pédagogie de l’intégration constitue la base méthodologique. L’élève est placé devant une situation complexe proche de celles de la vie. Le contexte, qui met en place une situation significative pour l’élève, est présenté dans sa globalité, l’élève, de manière autonome, doit mobiliser les ressources nécessaires à la résolution de la situation problème.
La complexité est liée au grand nombre de parties apparemment indépendantes l’une de l’autre (en ce sens que la connaissance de l’état d’une partie ne fournit pas ou fournit peu d’informations sur les autres), mais qui interagissent entre elles, de telle sorte que «le tout est supérieur à la somme des parties».
La réponse qui peut être apportée à la situation complexe est une réponse en forme de réseau qui se fonde sur les liens qui existent entre les éléments. C’est par la mobilisation et l’intégration interactive des différentes ressources qu’une solution peut être apportée à la situation complexe.

Il s’agit là d’une option du Sénégal qui a choisi l’Apc pour réformer son éducation de base dans le sens d’obtenir plus de pertinence des programmes et d’efficacité des stratégies d’enseignement-apprentissage. La généralisation est intervenue depuis 2013.

Dans l’évaluation certificative, une approche puriste se serait contentée de ne proposer que des situations complexes pour évaluer les compétences, mais pour l’instant, l’épreuve comprend aussi une section consacrée à l’évaluation des ressources, renvoyant à ce qu’on pourrait appeler des questions de cours.
Cette pédagogie de l’intégration s’organise autour de trois moments distincts et fortement liés :

• Dans un premier temps, l’élève acquiert des ressources (leçon après leçon : apprentissages ponctuels) ;

• Dans un deuxième temps, l’élève apprend à intégrer ces ressources dans des situations complexes (apprentissage de l’intégration) ;

• Dans un troisième temps, l’élève est évalué (situation d’intégration).
Dans l’apprentissage de l’intégration, comme dans l’évaluation, l’élève est confronté à des situations significatives d’intégration. Le problème du Cfee 2023 en est une.

On peut donc affirmer que le processus qui a abouti à cette épreuve du Cfee n’est pas inconnu des élèves. Les apprentissages fonctionnent de cette manière, toute l’année.

Des ressources nécessaires à la résolution du problème….
La résolution de ce problème fait appel à des connaissances précises, appelées ressources. On peut citer :
– Prendre une fraction d’un nombre ;
– Le sens et la pratique des quatre opérations (addition, soustraction, multiplication, division) ;
– Les différentes questions d’un problème (questions intermédiaires, questions finales) ;
– Lecture d’un énoncé et analyse des données (données utiles, données inutiles…) ;
– Les démarches de résolution de problème (démarche progressive, démarche régressive).

Toutes ces ressources ont fait l’objet de plusieurs leçons dans les classes. Nous faisons remarquer, par exemple, que l’objectif pédagogique «Identifier les questions intermédiaires d’un énoncé́ mathématique» est inscrit dès le CP dans nos programmes (Voir Guide pédagogique du curriculum de l’éducation de base, première étape, niveau 2).

Et, comme par hasard, on trouve dans ce guide de la troisième étape (CM1-CM2) page 233, programme officiel de l’enseignement élémentaire, ceci : «Ta tante (sic) veut acheter un terrain qui a la forme d’un rectangle surmonté d’un demi-cercle… Ce terrain est estimé à 80 000 F l’are. Ta tante effectue un premier versement égal aux 3/5 du prix d’achat total. Le reste de la somme à payer est majoré de 20 000 F…» Signalons, ici, que ce guide constitue la référence officielle de l’enseignant, le manuel scolaire étant un outil de passation du programme.

Du vocabulaire employé dans le problème…
Chaque discipline a son jargon spécifique, son champ lexical. Beaucoup d’enseignants abordent systématiquement les concepts relatifs à tel ou tel chapitre. On remarquera qu’en 1982 déjà, on employait «comptant», «crédit», «remise», «majoré». Un enseignant nous disait, à propos de cette polémique : «Peut-on parler d’achat et de vente sans les notions ou mots de vocabulaire tels que comptant, à crédit, majoration, rabais ?»

Le Professeur Mary Teuw Niane, dans son post sur Facebook, intitulé les mathématiques au Cfee 2023, corrobore notre analyse. Il dit ceci : «… Le sujet que j’ai trouvé sur Facebook ne présente pas à mon avis de difficulté mathématique particulière. La résolution des questions est assez linéaire. Elle ne fait pas appel à une astuce particulière ou à une intuition très difficile à trouver. La vraie difficulté est dans le vocabulaire employé. Est-ce que ce vocabulaire technique est au programme ? Si la réponse est oui, il n’y a pas de problème. Si la réponse est non, là il y a un vrai problème car c’est un sujet d’examen. Ce n’est pas un sujet de concours.»

De l’évaluation basée sur des critères indépendants les uns des autres…
Au nombre des principes régissant l’évaluation certificative selon l’Apc, on peut citer notamment l’indépendance des critères d’évaluation. En mathématiques, il y a le critère «pertinence» (l’évalué a choisi l’opération convenable) et la «justesse» (l’opération effectuée est juste) ; il peut engranger les points de l’un ou l’autre de ces critères à chaque fois. Exemple : montant de la remise
– (320 000 X5)/100 = 1600 F (il est pertinent car l’opération choisie est convenable, mais le résultat est faux)
– (320 000 x100)/5 = 6 400 000 F (il n’est pas pertinent car l’opération n’est pas convenable, mais le résultat de son opération est juste)
Malgré le caractère loufoque de son résultat, il prend les points réservés à la justesse. De plus, le correcteur est tenu de suivre l’élève avec son propre résultat. Le temps où l’élève avait 0 (zéro) dès qu’il fausse la première opération est révolu. L’évaluation devient plus rigoureuse et plus juste. Evaluer ne signifie pas sanctionner, mais extraire de la valeur.

Pour ne pas conclure…
Nous rappelons que l’apprentissage du raisonnement constitue une des finalités de l’enseignement des mathématiques ; et «les problèmes constituent des moyens privilégiés de formation à ce raisonnement».

Il faut éviter d’habituer nos enfants à chercher des solutions dans un grenier de problèmes. Le problème c’est normalement une situation nouvelle que l’élève cherche à résoudre par ses moyens intellectuels… Ce faisant, nous pouvons espérer que les lauréats sortant de l’école élémentaire seront dotés «d’un outil intellectuel leur permettant d’appréhender des situations nouvelles».
Kaba DIAKHATE
Inspecteur de l’éducation à la retraite
Kabadiakhate2@gmail.com